ML for Molecular Properties Prediction

Roi Naveiro (CUNEF)
Simón Rodríguez Santana (ICMAT)

Discovering new molecules - Process

  • Design of new molecule: countless applications in various sectors, e.g. pharmaceuticals and materials.

  • Pharma: average time discovery starts - market, 13 years. Outside pharma: 25 years

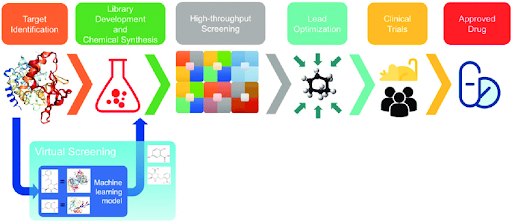
Discovering new molecules - Process

  • Crucial 1st step: generate pool of promising candidates

  • Daunting task (chemical space is huge and has complex structural constraints molecules)

The old and soon-to-be-old ways

  • Old way

    • Human experts propose, synthesize and test (in vitro)

  • Soon-to-be-old way: high throughput virtual screening (HTVS)

    • Predict properties through computational chemistry…
    • …leverage rapid ML-based property predictions

Problems with previous approaches

  • Just existing molecules are explored

  • Much time lost evaluating bad leads

  • Goal: traverse chemical space more “effectively”: reach optimal molecules with less evaluations than brute-force screening

Mathematically speaking

  • Combinatorial optimization problem

  • Often stochastic and multi-objective

  • Black-box objective functions

  • Black-box constraints

De novo design

The process of automatically proposing novel chemical structures that optimally satisfy desired properties

Two interrelated steps

  1. Optimally satisfy desired properties:
    Predictive models to forecast/approximate properties/ objective functions from chemical structure

  2. Automatically proposing novel chemical structures Automatic generation of molecules that optimize properties (predictions from first stage)

This workshop

  • Session 1: Predictive (QSAR) Models, with focus in low data regime

  • Session 2: Generative Models

  • Session 3: The Tailor’s Drawer (+ Case Study)

Predictive Models

Predictive models to forecast properties of molecules given structure, with focus on small data regime

  1. Computational representations of molecules

  2. An overview of predictive models for molecular properties

  3. Evaluating model performance

Representating molecules

Molecules are 3D QM objects with: nuclei with defined positions surrounded by electrons described by complex wave-functions

  • Digital encoding that serves as input to model

  • Uniqueness and invertibility

  • Trade-off: information lost vs complexity

    • 3D coord. representation (symmetries?)

    • More compact 2D (graph) representation

  • 1D, 2D and 3D Representations

1D Representations

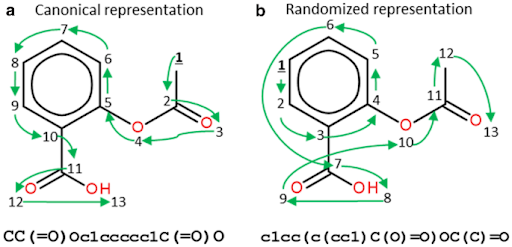
  • Simplified Molecular Input Line Entry System (SMILES)

  • Molecule as graph (bond length and conformational info lost)

  • Traverse graph

  • Generate Sequence of ASCII characters

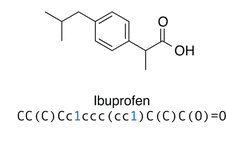
1D Representations

  • Non-Unique! Canonical SMILES

  • Tabular data:

    • One-Hot Encoding (NLP)
    • Molecular Descriptors (usual ML models)

Molecular Descriptors

2D Representations

  • Nodes represent atoms
  • Edges represent bonds
  • Nodes/Edges have associated features (atom number, bond type, etc.)
  • Capture connectivity!
  • Respect symmetries
  • Tailored algorithms (GNNs!)

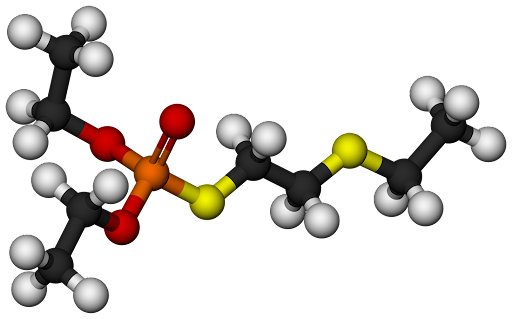
3D Representations

  • 3D point clouds: \(\mathcal{M} = \lbrace x_i, r_i \rbrace_{i=1}^p\), where \(x_i\) are features and \(r_i\) are coordinates

  • Minimal information lost (conformational preferences, bond lengths, etc.)

  • Tailored predictive algorithms that respect 3D translational and rotational invariance

An overview of predictive models for molecular properties

  • Molecular representation \(x\) and property \(y \in \mathbb{R}\)

  • Given training data \(\mathcal{D} = \lbrace x_i, y_i \rbrace_{i=1}^p\)…

  • … predictive regression model of \(y\) given \(x\).

  • Deterministic models - Point Forecasts

  • Probabilistic (Bayesian) models - Probabilistic Forecasts

Models for 1D representations - Descriptors

  • Usual desterministic models: linear regression, RF, XGBoost, SVR…

  • Low-data regime:

    • \(p \gg n\): need for regularization

    • Uncertainty is key \(\Rightarrow\) probabilistic (Bayesian) models

Models for 1D representations - Strings

  • One-hot encoding of SMILES representations

  • Deep Neural Nets: RNN, 1D Conv, Transformers

  • BNNs

    • Computationally expensive to train

    • Variational Inference: uncertainty underestimation Blei et. al. (2018)

Models for 2D molecular representations

  • Graph Neural Networks

  • Sequence of graph-to-graph blocks + output layer

  • (Infinitely) many architectures: Graph Networks Battaglia et. al. (2018)

GNNs (on a nutshell)

  • Functions on graph-structured data

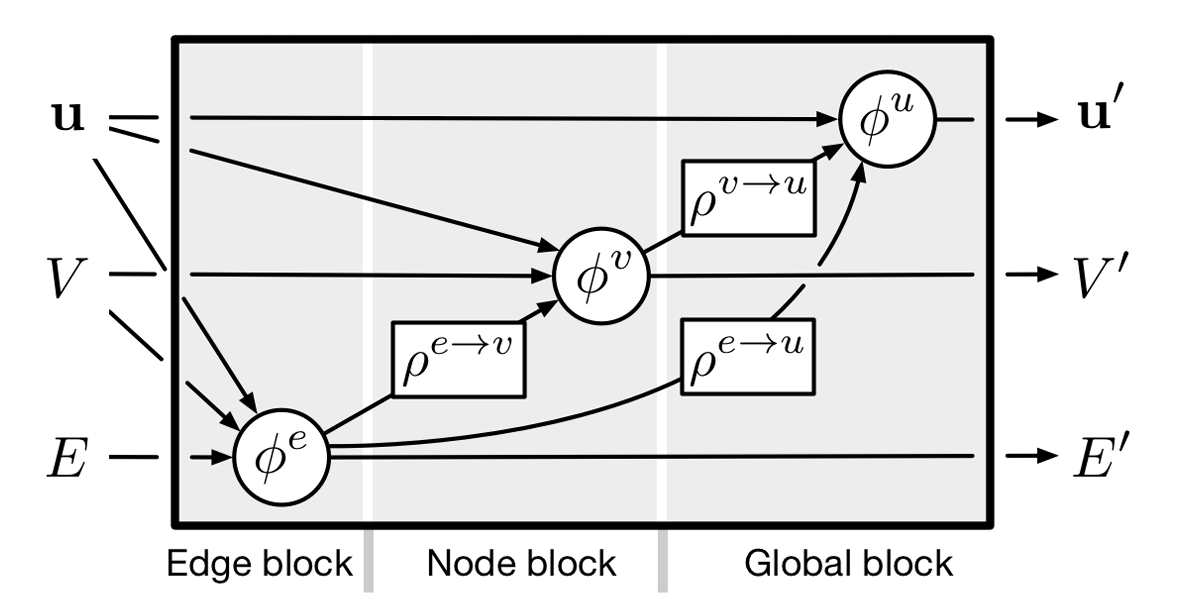
  • GN block (graph-to-graph map): primary computational unit in GNN

  • Graph \(N_v\) nodes and \(N_e\) edges: tuple \(G = (\textbf{u}, V, E)\)

    • \(\textbf{u}\): global attribute
    • \(V = \lbrace v_i \rbrace_{i=1:N^v}\): set of node attribute vectors
    • \(E = \lbrace (\textbf{e}_k, r_k, s_k)\rbrace_{k=1:N^e}\): set of edges. \(\textbf{e}_k\) edge attribute, \(r_k\) index of receiving node, and \(s_k\) is index of sending node.

GN Block

  • Edge update function \(\phi^e\)

  • Node update function \(\phi^v\)

  • Global update function \(\phi^u\).

  • \(\rho^{e\rightarrow v}\): aggregates edge attributes per node

  • \(\rho^{e\rightarrow u}\): aggregates edge attributes globally

  • \(\rho^{v\rightarrow u}\): aggregates node attributes globally.

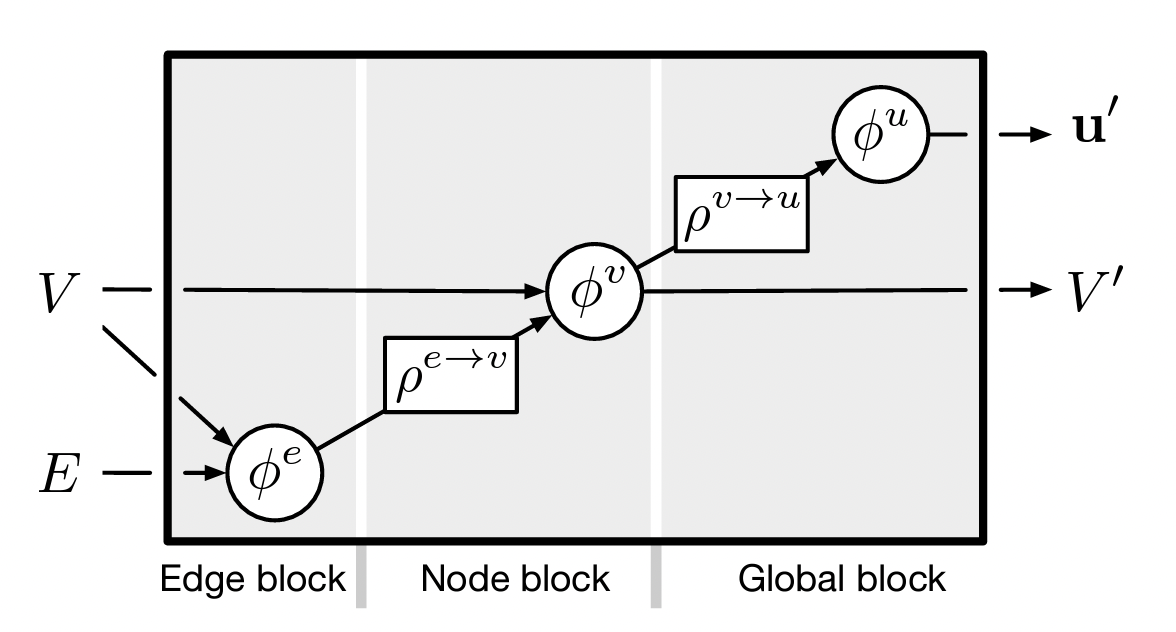
GN Block - Computations

GN Block - Computations

MPNN Block - Computations

GNN

  • Various parametric forms for functions

  • Multilayer perceptrons for the update functions and sums for the aggregate functions

  • GN blocks can be concatenated

  • Output layer of GNN depends on the task

GNN Workflow

The entire architecture can be summarized as follows:

  1. Encode the input graph using independent node and edge update functions to match the internal node and edge feature sizes

  2. Apply multiple GN blocks

  3. Use an output layer to map the updated global features to a property prediction

Once the architecture is defined, the parameters can be optimized using standard optimizers and loss functions.

Models for 3D molecular representations

  • Geometric Neural Networks

  • (Again) many architectures

  • In a Geometric Net Block we update:

    • Node features, s.t. updated features are invariant to 3D translations and rotations

    • Node coordinates, s.t. updated coordinates are equivariant to 3D translations and rotations

  • \(E(n)\) equivariant graph neural nets Satorras et. al. (2022)

E(n) equivariant GNNs

  • Refinement of MPNN

  • \(G = (V, E)\)

  • In addition to node features, coordinates: \(V = \lbrace v_i, x_i \rbrace_{i=1:N_{v}}\).

In a MPNN

  1. \(\forall\) edges \(k\), \(\textbf{e}'_k = \phi^{e} (\textbf{e}_k, \textbf{v}_{r_k}, \textbf{v}_{s_k})\)

  2. \(\forall\) nodes \(i\)

    • \(E'_i = \lbrace (\textbf{e}'_k, r_k, s_k) \rbrace_{r_k = i}\)
    • \(\bf{\overline{e}'_i} = \rho^{e\rightarrow v} (E'_i)\)
    • \(\textbf{v}'_i = \phi^{v} (\bf{\overline{e}'_i}, \textbf{v}_{i})\)
  1. \(V' = \lbrace \textbf{v}'_i \rbrace_{i=1:N^v}\)
  2. \(\bf{\overline{v}}' = \rho^{v\rightarrow u} (V')\)
  3. \(\textbf{u}' = \phi^u (\bf{\overline{v}'})\).

E(n) equivariante GNNs

  1. \(\forall\) edges \(k\), \(\textbf{e}'_k = \phi^{e} (\textbf{e}_k, \textbf{v}_{r_k}, \textbf{v}_{s_k}, \color{red}{\Vert x_{r_k} - x_{s_k} \Vert ^2} )\)

  2. \(\forall\) nodes \(i\)

    • \(E'_i = \lbrace (\textbf{e}'_k, r_k, s_k) \rbrace_{r_k = i}\)
    • \(\bf{\overline{e}'_i} = \rho^{e\rightarrow v} (E'_i)\)
    • \(\textbf{v}'_i = \phi^{v} (\bf{\overline{e}'_i}, \textbf{v}_{i})\)
    • \(\color{red}{x'_i = x_i + C \sum_{k;~r_k = i} (x_i - x_{s_k}) \cdot \phi^x (\textbf{e}'_k)}\)
  1. \(V' = \lbrace \textbf{v}'_i \rbrace_{i=1:N^v}\)
  2. \(\bf{\overline{v}}' = \rho^{v\rightarrow u} (V')\)
  3. \(\textbf{u}' = \phi^u (\bf{\overline{v}}')\).

Evaluating model performance - Point Predictions

Usual metrics for regression

  • RMSE

  • MAE

  • MAPE

  • \(R^2\)

Evaluating quality of probabilistic predictions

Evaluating quality of probabilistic predictions

  • Idea: create \((100 \cdot q)\)% prediction intervals for the property prediction of every molecules in a test set.

  • \(C(q)\) is the proportion of the molecules in the test set whose property value is in the interval calculated for such molecule.

    • If \(C(q) = q\) we say that the model is well calibrated.

    • If \(C(q) < q\) we say that the model is overconfident.

    • If \(C(q) > q\) we say that the model is underconfident.

Evaluating quality of probabilistic predictions

Hands-on!