De-novo Molecular Design

Roi Naveiro (CUNEF)
Simón Rodríguez Santana (ICMAT)

Molecular design problem

  • Design of new molecules is time and resource intensive task
  • Generating promising candidates is one of the main bottlenecks
  • Old approach: Expert propose + synthesize + measure candidates in vitro
  • Soon-to-be-old way: High throughput virtual screening (HTVS)

Traditional molecular design

Virtual Screening (VS): Brute-force evaluation of huge libraries of compounds to identify structures that improve desired properties (e.g. drug-likeness)

  • Structures known a priori
  • Although databases are huge, they represent a small portion of the total chemical space
  • Concerns about predictive validity and redundancy (Scannell et al., 2016)

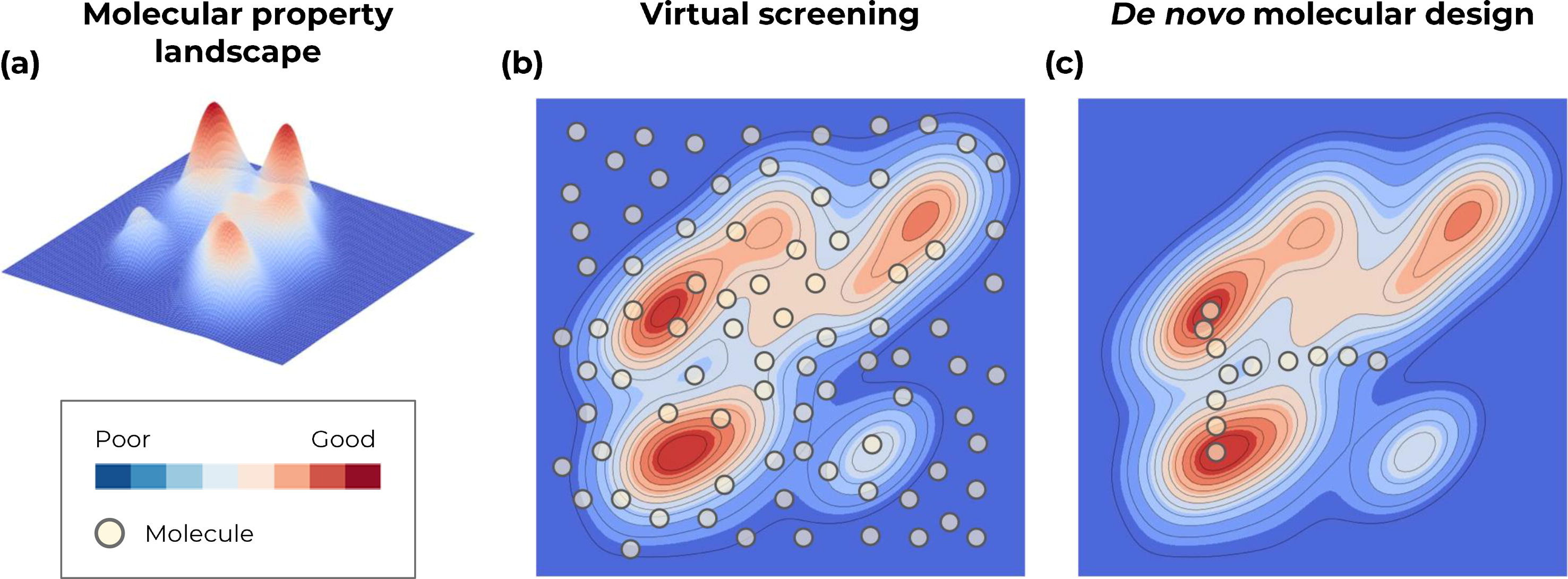
De-novo molecular design

Main goal: Traverse the chemical space more effectively (better molecules in less evaluations)

  • AI assisted de-novo design \(\rightarrow\) Process of automatically proposing novel chemical structures that optimally satisfy desired properties

De-novo molecular design

Generate compounds in a directed manner

  • Reach optimal chemical solutions in fewer steps than VS
  • Explore different acceptable regions of chemical space for a given objective (exploration vs. exploitation)

Recap - molecule encoding


  • Molecules are 3D QM objects
  • Encoding enables to capture certain information
  • Trade-off: information loss vs. complexity

Recap - property prediction

Select the model depending on the encoding information

  • 1D: Smiles, 1-hot, descriptors, etc.
    • Deterministic and Bayesian models
    • Deep NNs (+ Bayesian version)
  • 2D: Graphs (GNNs)
  • 3D: Point clouds (Geometric NNs)

Performance measures (RMSE, \(R^2\), etc.) + assessment of probabilistic predictions

Generative and discriminative models

De-novo design is also referred to as generative chemistry

  • Discriminative models learn decision boundaries

  • Generative models model the probability distribution of each class

    \(\rightarrow\) Can be instantiated to generate new examples (!)


Not the only way to obtain new compounds…

Requirements

  • Validity: Adherence to chemical principles (e.g. valency)
  • Uniqueness: Rate of duplicates by the model
  • Diversity: Scope of the chemotypes generated
  • Novelty: Presence of generated molecules in databases
  • Similarity: Similarity between generated molecules and training data
  • Synthetic feasibility: Lab-related synthesizability

Untargetted vs. targetted (extra metric to optimize, e.g. QED, PlogP and many more)

Generative models


Targetted generation depends on having a proper characterization of the property of interest

  • Property prediction models serve to define an objective function (Session 1)
    • Navigate a complex search space
  • Gradient-based vs. gradient-free methods

Gradient-based vs. gradient-free

Gradient-based: Models that use the gradient of the objective function to perform optimization

  • Training requires fitting parameters using data corpuses
  • Usually require lots of data
  • E.g.: NN-based approaches (s.a. VAEs)

Gradient-free: Metaheuristic models, based on stochastic population optimization

  • “Rule-based” approaches
  • E.g.: Evolutionary algorithms

Chemical representations

Chemical representation tailored for each case depending on the data, objective and resources available

  • Atomic level: Encode information for each atom and bond
    • E.g.: Atom-wise SMILES, graph, 3D coordinates…
  • Fragment level: Functional groups, substructures fixed
    • E.g.: Benzene as a single group
  • Reaction level: Target molecule as product of reactant and reactions conditions
    • E.g.: Combinations from library of reactions

Model zoo


Atom based Fragment based Reaction based
Gradient free EvoMol*
GB-GA		 CReM AutoGrow4
Gradient based ChemVAE*
EDM*
PaccMannRL
GraphAF		 JT-VAE DoG

Many (many) more… VLS3D list of resources

Gradient based models

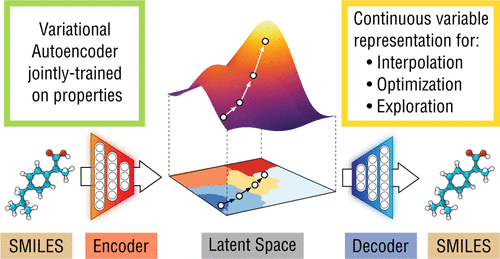
ChemVAE

Originally introduced in Bombarelli et al. (2018)

  • Combines a Variational Autoencoder and a property predictor
  • Meaningful and contiuous latent space
  • Uses Bayesian optimization to efficiently explore the latent space
  • Led to expansion of VAEs in molecular design

Extension of the ideas from Generative Adversarial Networks (GANs) and autoencoders

Autoencoder

AE: Hourglass-structured NN that encodes and decodes the input information, consisting on an encoder, \(f_\theta(x)\), decoder, \(g_\phi(z)\), and the latent space, \(z\)

Attempts to learn the identity function, i.e. \[ \text{VAE} = g_\phi \circ f_\theta \, \quad s.t. \quad \text{VAE}^*(x) = g_\phi(f_\theta(x)) = x \]

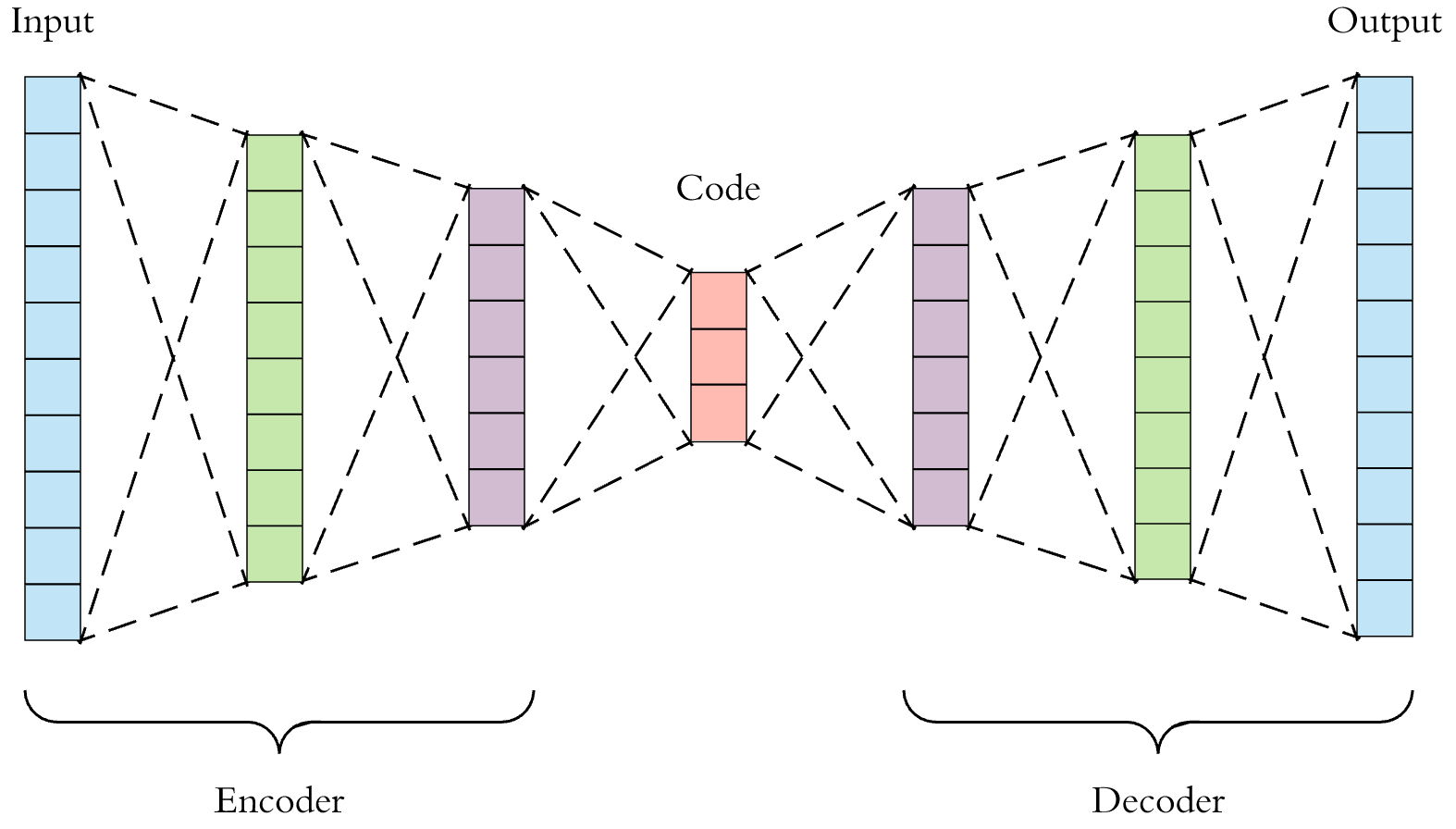
Autoencoder

  • Encoder: Maps the input to the latent space \(f_\theta(x) = z\)
  • Decoder: Maps latent space to original space \(g_\phi(z) = \hat{x}\)
  • Latent space: Low-dimensional representation of \(x\) (\(z\))

Minimize the reconstruction error (\(\epsilon\)): \[ \arg \min_{\theta,\phi} \epsilon(x, \hat{x}) \]

\(\hat{x} \simeq x\) \(\Rightarrow\) Model encodes/decodes correctly

Autoencoder

AE can be seen as generative models

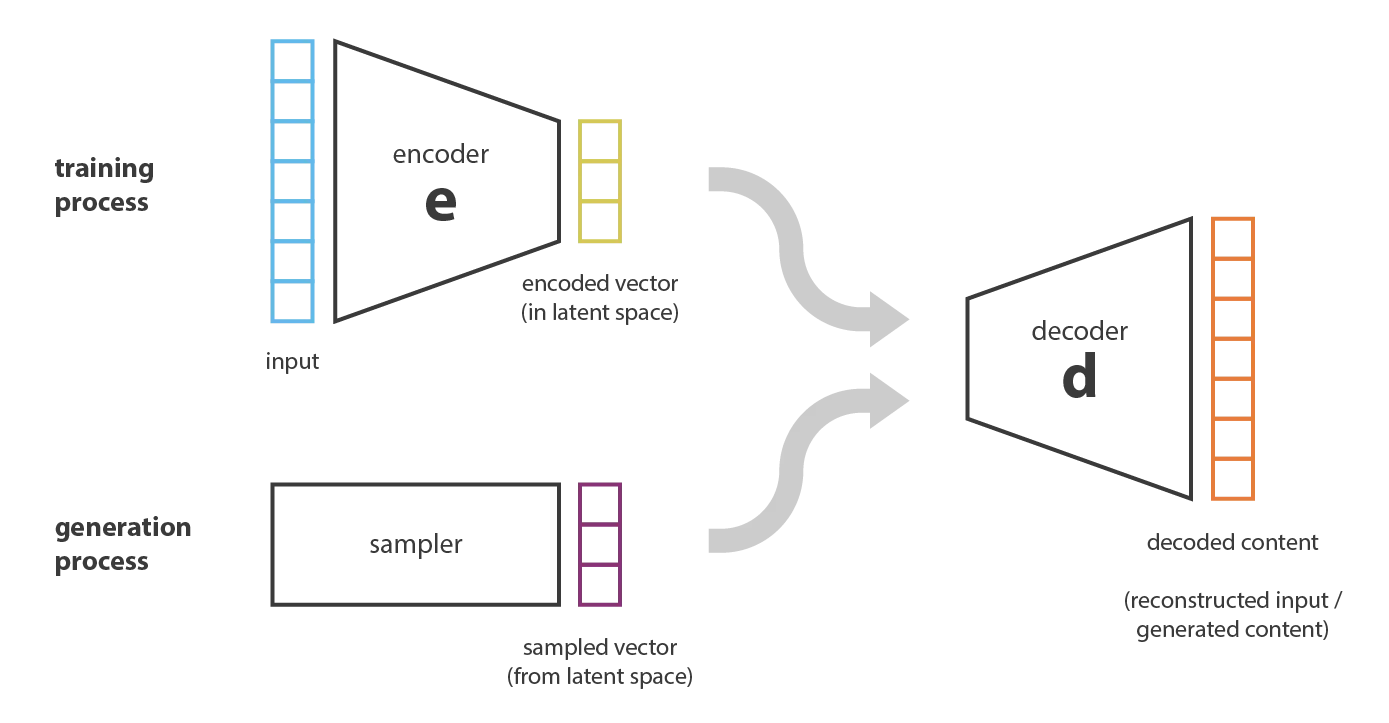
Latent space difficult to navigate

Variational Autoencoders

VAE: Adds stochasticity to the encoding \(\rightarrow\) Regularize latent space

  • Instead of encoding to a point, do it to a distribution \(p(z|x)\)
  • Sample from the distribution \(z \sim p(z|x)\) and decompose

\[ Loss = \epsilon(x,\hat{x}) + regularizer \]

The regularization forces latent encoding to ressemble a prior: \[ p(z) = \mathcal{N}(0, I) \]

Variational Autoencoders

The encoded data will follow \[ z \sim q(z|x) = \mathcal{N}(\mu_x, \sigma_x) \]

where \(\mu_x\) and \(\sigma_x\) are given by \(f_\theta(x)\), which can be seen as \[ \mu_x = f^1_\theta(x), \quad \sigma_x = f^2_\theta(x) \] being \(f^1\) and \(f^2\) the first and second half of the units of the latent layer

Variational Autoencoders

KL divergence as regularizer (closed form solution) \[ KL(q(z|x)|p(z)) = \sum_{i=1}^n (\sigma_{x,i})^2 + (\mu_{x,i})^2 - log(\sigma_{x,i})-1 \]

Adding noise, we sample from the latent space and decode it

ChemVAE

ChemVAE: VAE + property predictor

\[ \mathcal{L}_{\text{VAE}} = \epsilon(x, \hat{x}) + KL(q(z|x)|p(z)) + \mathcal{L}_P(x,\hat{x}) \] with \(\mathcal{L}_P(x,\hat{x})\) the property prediction error

  • Train all elements together
  • Sort the latent space to encode the property information
  • Bayesian optimization to move in latent space
    • Assume local and smooth behavior

ChemVAE

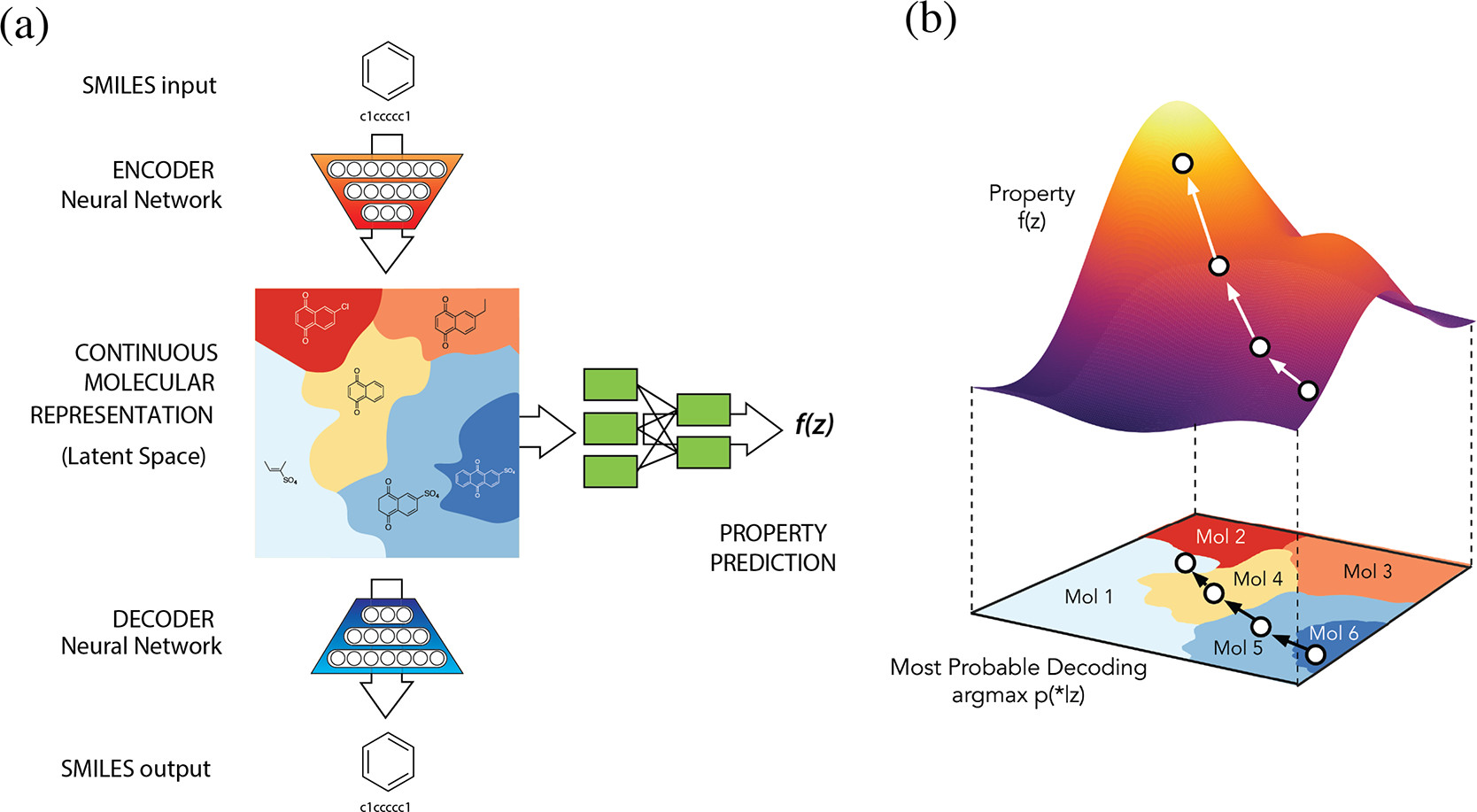
Fig: (a) ChemVAE architecture (b) Property optimization via BO

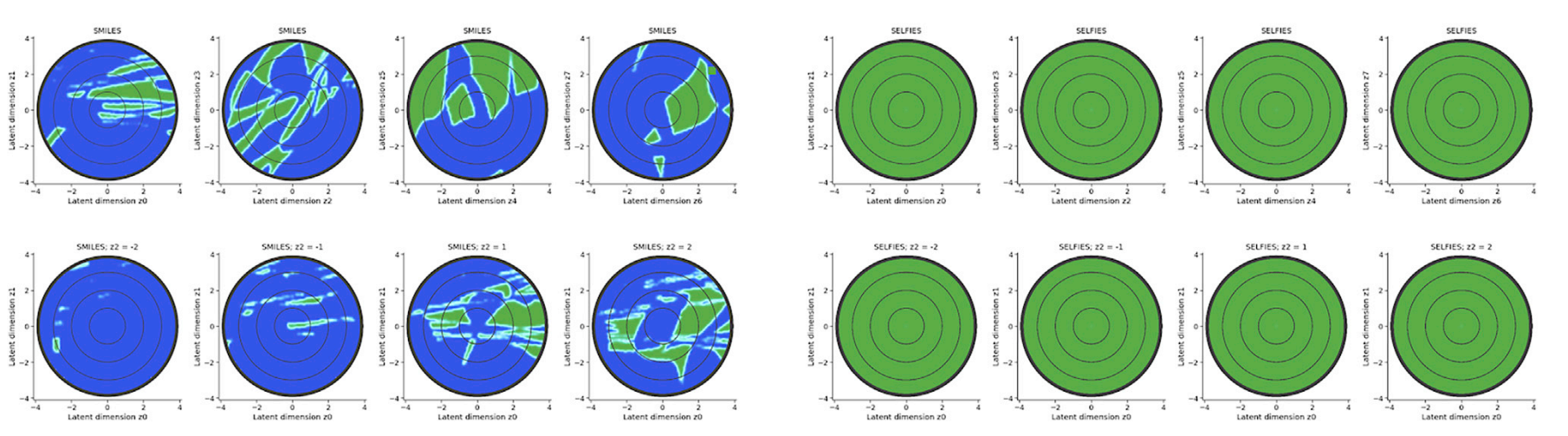
ChemVAE - Latent space

Local behavior + interpolation between compounds possible

ChemVAE - Latent space

Property prediction crucial for meaningful latent space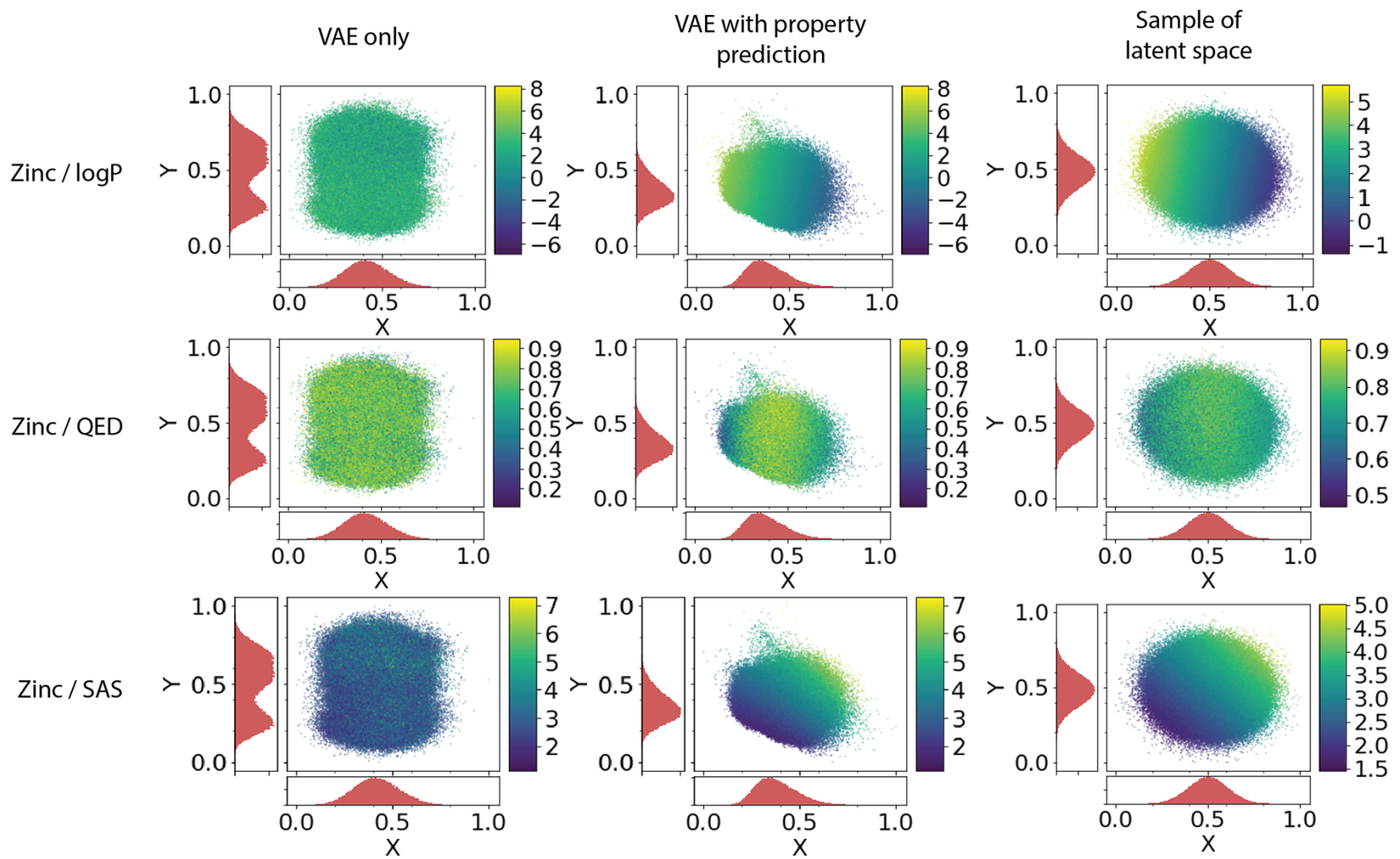

ChemVAE - Comments

  • Lead to many other VAE-based methods
  • Generates compounds that are hard to synthesize
  • Latent space with very low validity (SMILES encoding)
    • Use SELFIES encoding

ChemVAE - Hands on!




generative_models/ variational_autoencoder/ VAE.ipynb


Only a brief introduction though… Check the original repo for extended functionality

Other models

VAE-based: Recent interest in using reinforcement learning

  • PaccMannRL: RL-based approach using 2 VAEs
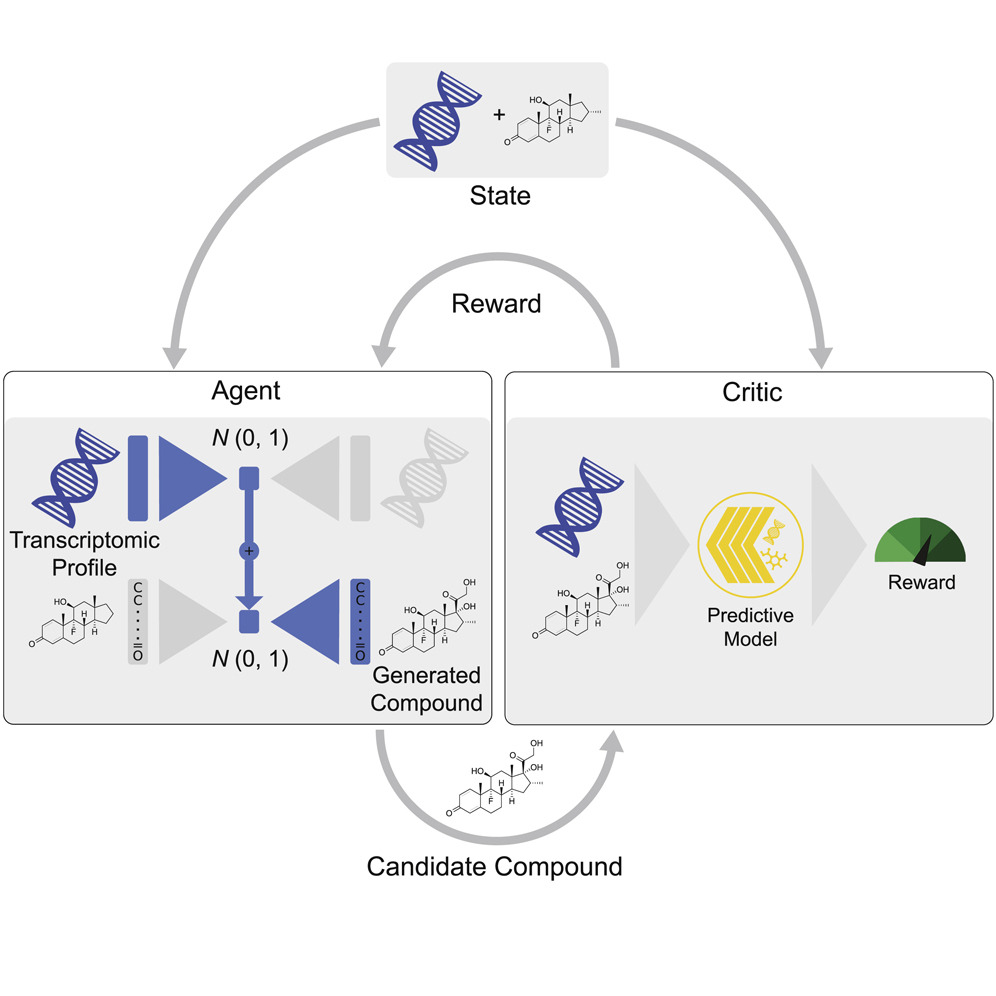
    • Used for SARS-CoV-2 drug discovery (paper)

Diffusion models

EDM: Equivariant diffusion model for 3D molecule generation

  • Use a diffusion process instead of a VAE
  • \(E(3)\) symmetries: rotation, traslation and reflections

The same principle behind Stable Diffusion

Diffusion models - diffusion process

Diffusion model learns denoising processes (opposite of a diffusion process)

\(\rightarrow\) progressively add Gaussian noise (\(z_t\)) to signal (\(x\)) \[ q(z_t|x) = \mathcal{N}(z_t|\alpha_tx_t, \sigma_t^2I) \] with \(\alpha_0 \approx 1\) and \(\alpha_T \approx 0\) and \(\sigma_t\) the added noise level

Diffusion models - diffusion process

The diffusion process is Markovian with transition distribution \[ q(z_t|z_s) = \mathcal{N}(z_t|\alpha_{t|s}z_s, \sigma_{t|s}^2I)\,, \quad \forall t>s \] with \(\alpha_{t|s} = \alpha_t/\alpha_s\) and \(\sigma_{t|s}^2 = \sigma_t^2 - \alpha_{t|s}^2\sigma_s^2\)

The complete process can be given by: \[ \begin{gathered} q(z_0, z_1, \cdots, z_T|x) = q(z_0|x) \textstyle{\prod_{t=1}^T} q(z_t|z_{t-1}) \\ q(z_s|x, z_t) = \mathcal{N}(z_s|\mu_{t \rightarrow s}(x, z_t), \,\sigma_{t \rightarrow s}^2I) \end{gathered} \] with \(\mu_{t \rightarrow s}(x, z_t)\) and \(\sigma_{t \rightarrow s}^2\) in terms of \(\alpha\)’s , \(\sigma\)’s, \(x\) and \(z\)

EDM

  • We know the distribution of the diffusion process at each \(t\)
    • Noise applied to atom types and other properties (\(h\)) using their encodings
  • Generative process: \(\hat{x} = \phi(z_t, t)\) (denoising \(z_t\))
    • \(\phi\) is an \(E(3)\) equivariant graph NN (session 1)
  • We undo the path step-by-step minimizing \[ \textstyle{\sum_{t=1}^T} E_{\epsilon_t \sim \mathcal{N}_{xh}(0, I)} \left[ \textstyle{\frac{1}{2}} w(t) ||\epsilon_t - \hat{\epsilon}_t||^2 \right] \] with \(\hat{\epsilon}_t = \phi(z_t,t)\), \(\epsilon_t\) the \(t\)-step diff. and \(w(t)\) via \(\alpha_t\) and \(\sigma_t^2\)

EDM - Overview



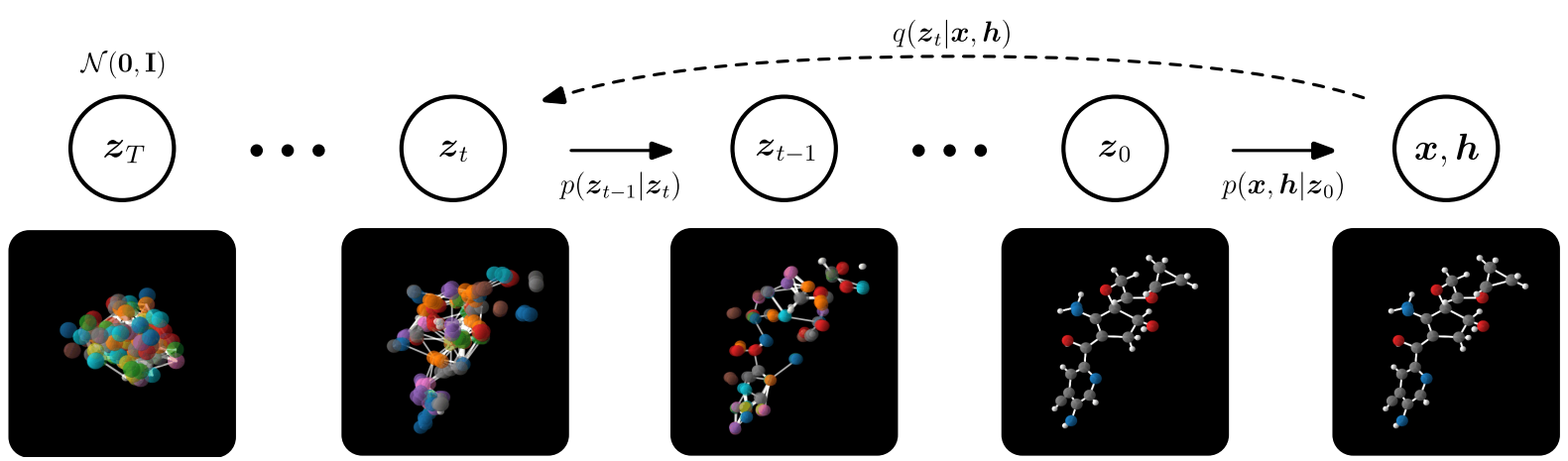
Similar to VAE approach, but now only decoding and latent space as pure noise

EDM - Computations

EDM - Conditional generation


EDM performs property optimization with a simple extension of \(\phi\) into \(\phi(z_t, [t, c])\), with \(c\) a property of interest

  • Molecules with increasing polarizability (\(\alpha\)), given above

EDM - Hands on!


generative_models/ diffusion/DIFFUSION.ipynb

Gradient free models

Evolutionary algorithms

Key idea:

Population of individuals (states) in which the fittest (highest valued state) produce offspring (successor states) that populate the next generation in a process of recombination and mutation.

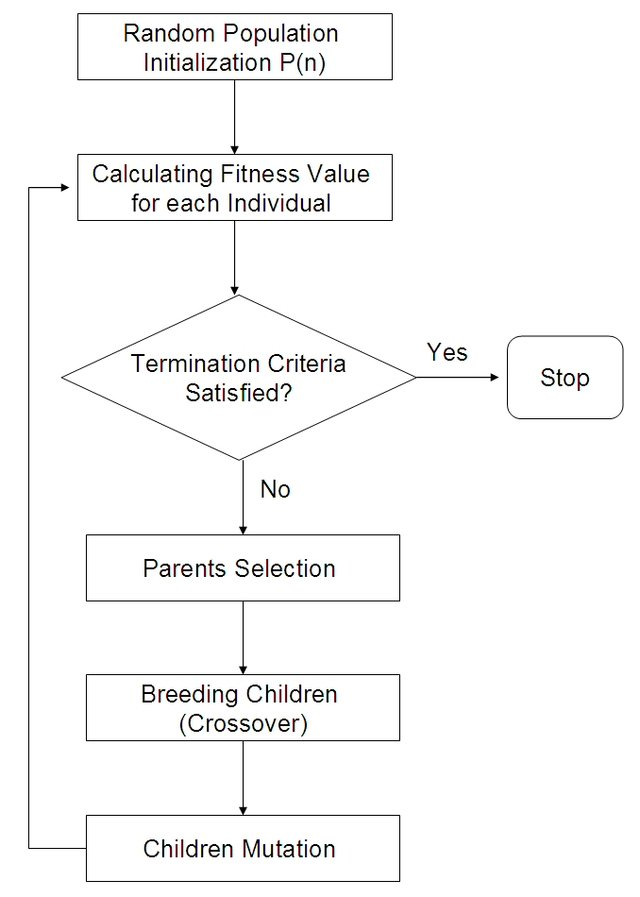
Evolutionary algorithms

Many different evolutionary algorithms, they mostly vary on their setup regarding common criteria:

  • Population size
  • Representation of each individual
    • Strings (s.a. ATGC for genes), sequences of real numbers (evolution strategies) or even computer programs (genetic programming)
  • Mixing number (\(\rho\)): number of parents that form offspring (commonly 2, stochastic beam search \(\rho = 1\))

Evolutionary algorithms

Many different evolutionary algorithms, they mostly vary on their setup regarding common criteria:

  • Selection process: Select parents for the next generation.
    Different options:
    • Select from all individuals with probability proportional to their fitness score.
    • Randomly select \(n\) individuals (\(n > ρ\)), and then select the ρ most fit ones as parents.
    • (many more)

Evolutionary algorithms

Many different evolutionary algorithms, they mostly vary on their setup regarding common criteria:

  • Recombination procedure
    • E.g. \(\rho = 2\), select random crossover point to recombine two parents into two children

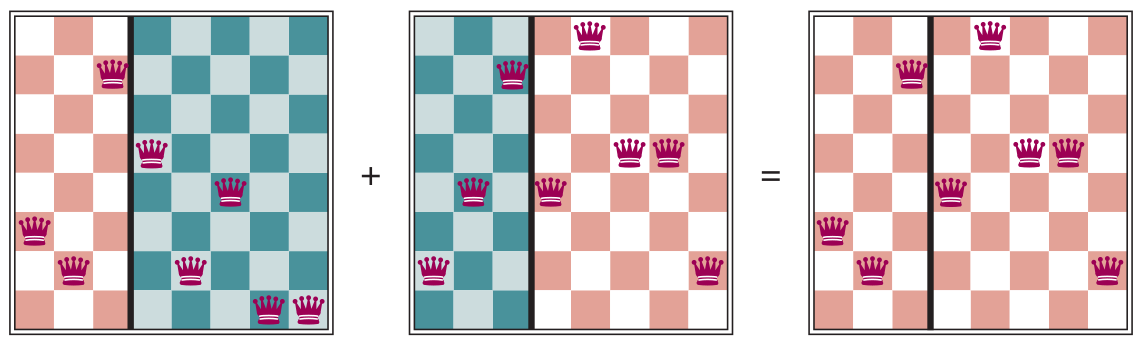
Evolutionary algorithms

Many different evolutionary algorithms, they mostly vary on their setup regarding common criteria:

  • Mutation rate, or how often offspring have random mutations representation
  • Next generation makeup:
    • Just the new offspring
    • Include a few top-scoring parents from the previous generation (elitism)
    • Culling (individuals below a given threshold are discarded)

Evolutionary algorithms


Example: (a) Rank population by fitness levels (b), resulting in pairs (c) from mating and producing offspring (d) which are subject to mutations (e)

Evolutionary algorithms


Previous case:

Child gets the first three digits from the \(1^{st}\) parent (327) and the remaining five from the \(2^{nd}\) parent (48552)
(no mutation here)

Evolutionary algorithms


Schema: Structure in which some positions are left unspecified

  • Instances: Strings that match the schema
  • Example: 327\(^{*****}\) (all instances beggining with 3, 2, and 7)
  • Useful to maintain an interesting piece in evolutionary process

EvoMol

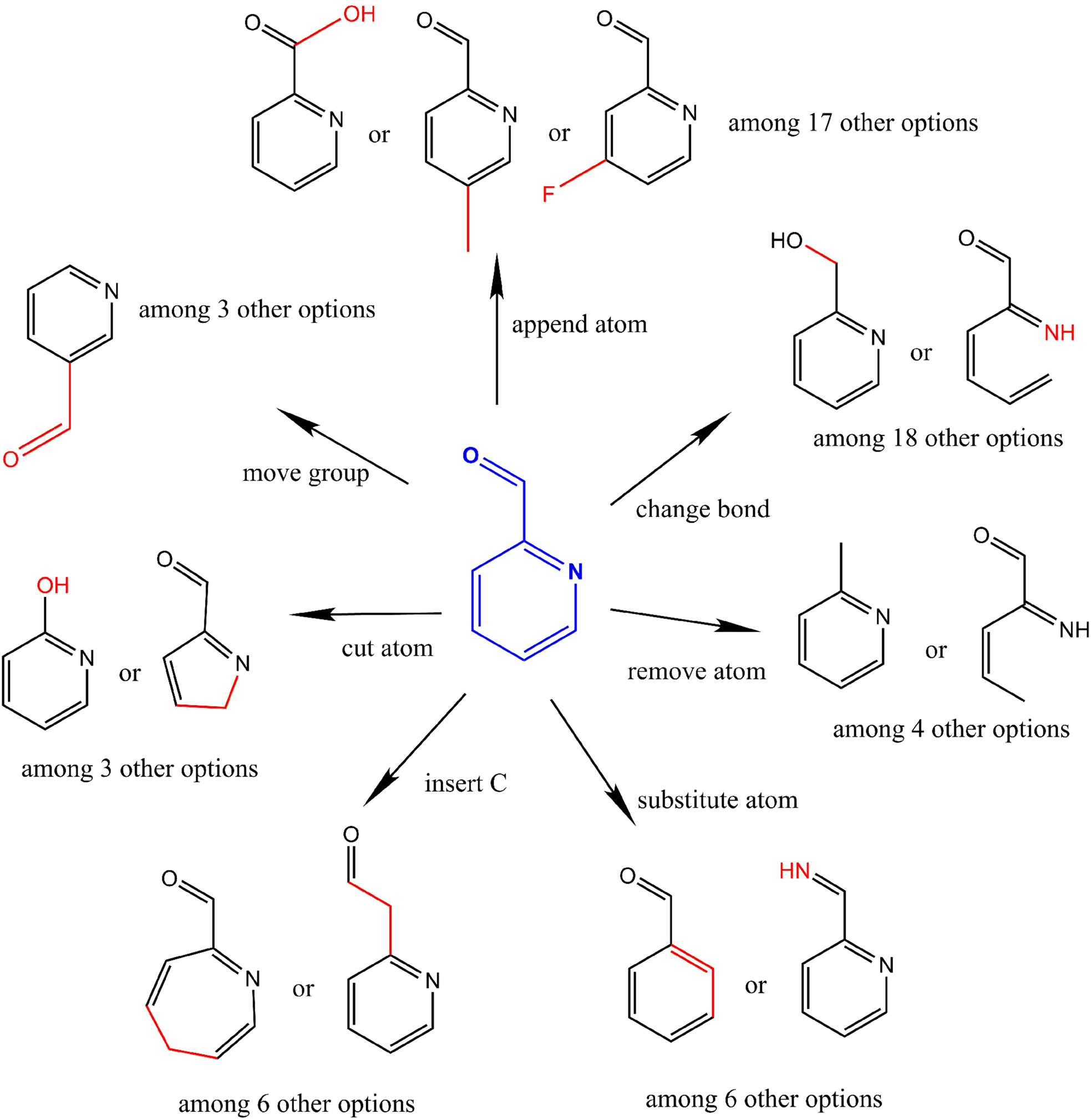
EvoMol - Impletation

EvoMol - Hands on!



generative_models/ evolutionary_algorithm/GENETIC.ipynb