Machine Learning: a Probabilistic Perspective

Roi Naveiro (CUNEF, AItenea Biotech SL)

Why now?

Over 2017 and 2018 alone, 90 percent of the data in the world was generated.

In addition to data

• Computational power

• Algorithmic advances

  • [Powerful models (Architectures)]

  • [Stochastic Gradient Descent]

  • [Automatic Differentiation]

Machine Learning

“Machine learning (ML) is a field of study in artificial intelligence concerned with the development and study of statistical algorithms that can learn from data and generalize to unseen data, and thus perform tasks without explicit instructions.”

— Source: Wikipedia

Machine Learning - Learn?

A computer program is said to learn from experience E with respect to some class of tasks T and performance measure P, if its performance at tasks in T, as measured by P, improves with experience E.

— Source: Tom M. Mitchell

Machine Learning Types

Depending on experience and task

• Supervised learning

• Unsupervised learning

• Reinforcenment learning

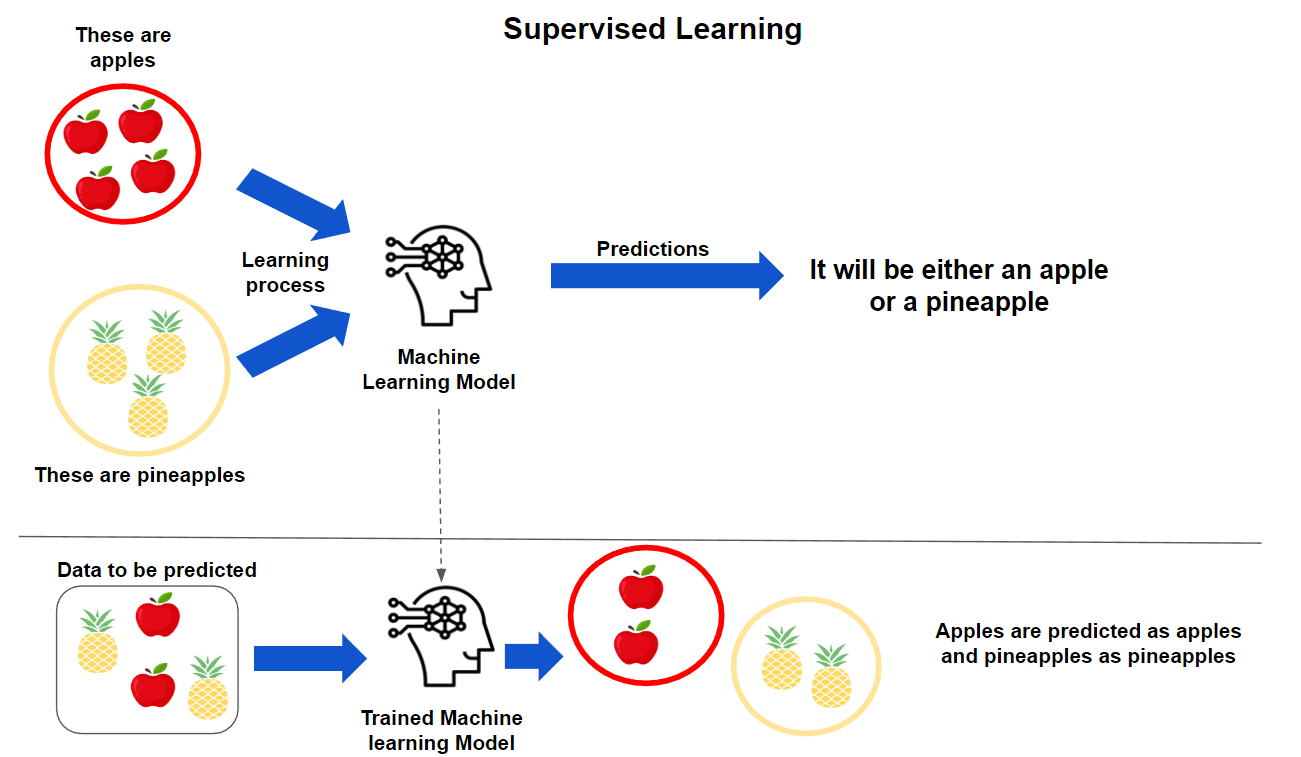
Supervised Learning

• We are given a labelled dataset \(\mathcal{D} = \lbrace \boldsymbol{x}_i, y_i \rbrace_{i=1}^N\), where \(\boldsymbol{x}_i \in \mathcal{X}\) and \(y \in \mathcal{Y}\)

• Goal: given unobserved instance \(\boldsymbol{x'}\), predict its \(y\)

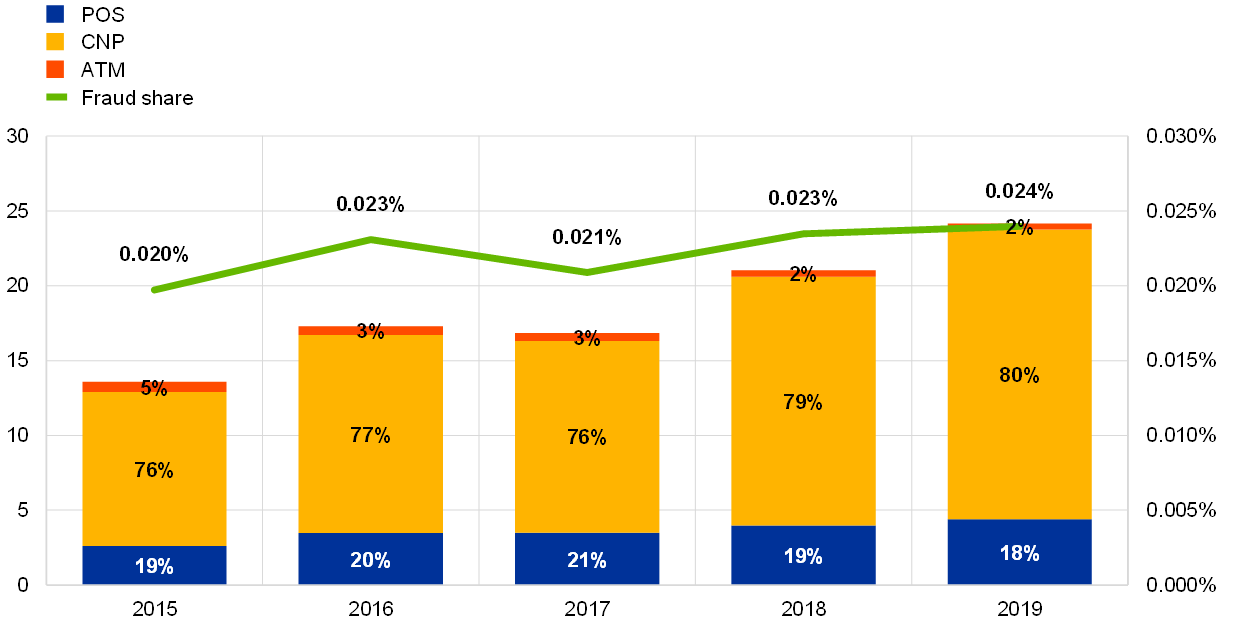
SL - Fraud Detection

Use known transactions to learn function from transaction characteristics to probability of fraud

SL - Automated Driving Systems

Use labelled images to learn function from image to sign

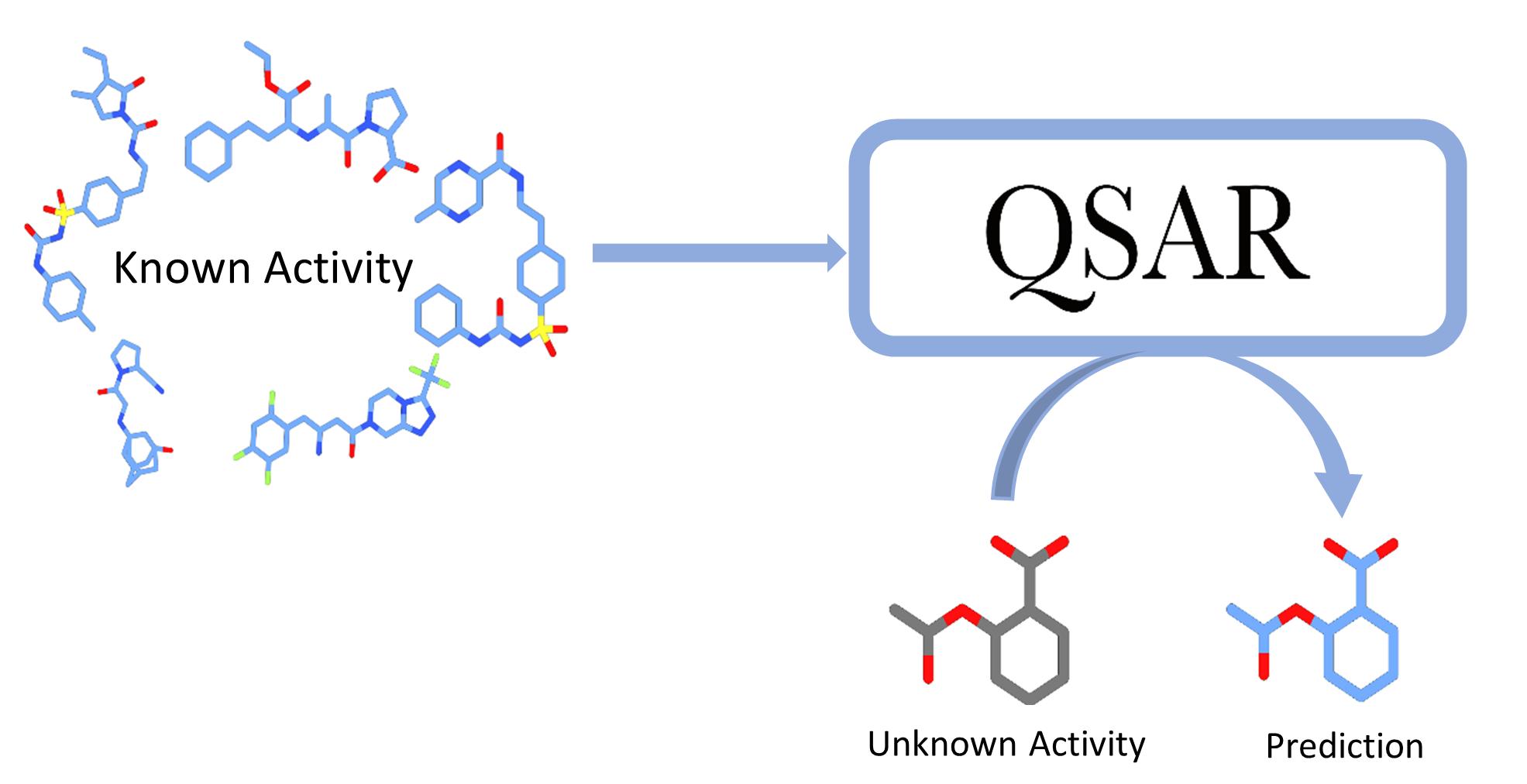
SL - Property prediction

Use known molecules to learn function from structure to property value

SL - How can we do it?

• We need to assume a parametric probabilistic model

\[ \pi_{w}( y \vert \boldsymbol{x}) \]

• Use training data \(\mathcal{D} = \lbrace \boldsymbol{x}_i, y_i \rbrace_{i=1}^N\) to find best parameters \(w^*\)

• Given new instance \(\boldsymbol{x'}\), output \(y\) with highest

\[ \pi_{w}( y \vert \boldsymbol{x'}) \]

Machine Learning - Learn?

A computer program is said to learn from experience E with respect to some class of tasks T and performance measure P, if its performance at tasks in T, as measured by P, improves with experience E.

— Source: Tom M. Mitchell

Supervised Learning - Ingredients

• Labelled data: \(\mathcal{D}\) (Experience, Task)
  
  

• Probabilistic Model: \(\pi_{w}( y \vert \boldsymbol{x})\) (Computer Program)
  
  

• Training approach:

  • Way to measure how good the model is (Performance)
  • Adapt \(w\) to improve such performance

Example: linear regression

• Data \(\mathcal{D} = \lbrace \boldsymbol{x}_i, y_i \rbrace_{i=1}^N\) where \(\mathcal{x}_i = (x_{i1}, x_{i2}, \dots, x_{ip})\)

• Model:

\[ \pi_{w}( y \vert \boldsymbol{x}) = \mathcal{N}(w_1 x_{i1} + \dots w_p x_{ip}, \sigma) \]

Example: linear regression

• Training approach:

  • Maximize likelihood given dataset \(\mathcal{D} = \lbrace \boldsymbol{x}_i, y_i \rbrace_{i=1}^N\)

    \[ \max_{w_1, \dots, w_p}\prod_{i=1}^N \pi_{w}( y_i \vert \boldsymbol{x}_i) \]

  • Equivalent to minimizing sum-of-squares \[ \min_{w_1, \dots, w_p} \sum_{i=1}^N \left(y_i - \hat{y}_i \right)^2, ~~~~~ \hat{y}=w_1 x_{i1} + \dots w_p x_{ip} \]

Supervised Learning - Ingredients

• Labelled data: \(\mathcal{D}\) (Experience, Task)
  
  

• Probabilistic Model: \(\pi_{w}( y \vert \boldsymbol{x})\) (Computer Program)
  
  

• Training approach:

  • Way to measure how good the model is (Performance)
  • Adapt \(w\) to improve such performance

General Training approach

Assume we have a probabilistic model \(\pi_{w}( y \vert \boldsymbol{x})\) and a training data \(\mathcal{D} = \lbrace \boldsymbol{x}_i, y_i \rbrace_{i=1}^N\)

• Find \(w^*\) solving \[ \max_{w}\prod_{i=1}^N \pi_w( y_i \vert \boldsymbol{x}_i) \]

• Same as minimizing negative log-likelihood

  \[ L(\mathcal{D}, w) = \sum_{i=1}^N -\log \pi_{w}( y_i \vert \boldsymbol{x}_i) = \sum_{i=1}^N \ell (y_i, \boldsymbol{x}_i, w) \]

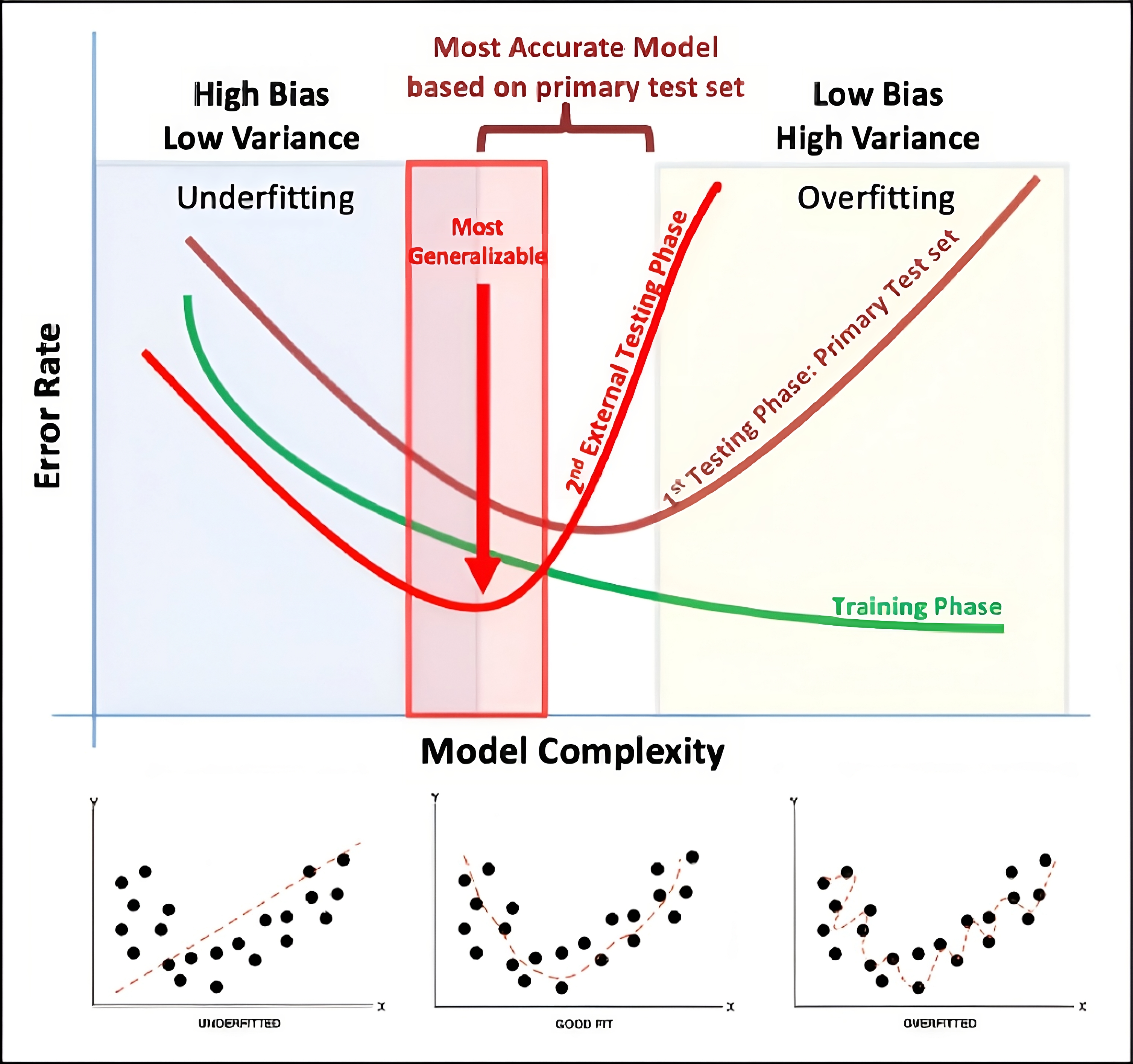
Training approach - Bias-Variance

Training approach - Regularization

Many approaches to solve this:

1. Modify loss: \[ L(\mathcal{D}, w) = \sum_{i=1}^N \ell (y_i, \boldsymbol{x}_i, w) + \lambda \Vert w \Vert \]

2. More data

3. Modify the optimizer

Training approach - Optimizer

Once we have loss function, how to find \(w^*\)?

• Analytically, almost never possible

• Numerically! Gradient Descent: follow the gradient

  \[ w_{t+1} = w_t - \eta_{t} \cdot \nabla_w L(\mathcal{D}, w) \]

• Under some conditions, this converges to optimal \(w\)… or a good enough one

Training approach - Optimizer

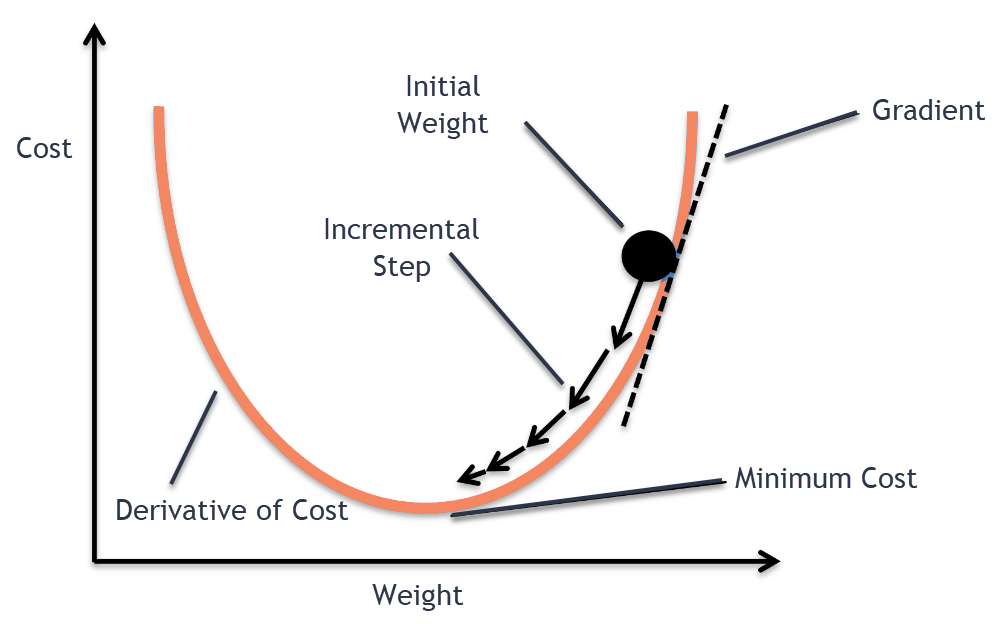
Training approach - Optimizer

[Stochastic Gradient Descent] \[ \nabla_w L(\mathcal{D}, w) = \sum_{i=1}^N \nabla_w \ell (y_i, \boldsymbol{x}_i, w) \approx \nabla_w \ell (y_k, \boldsymbol{x}_k, w) \]

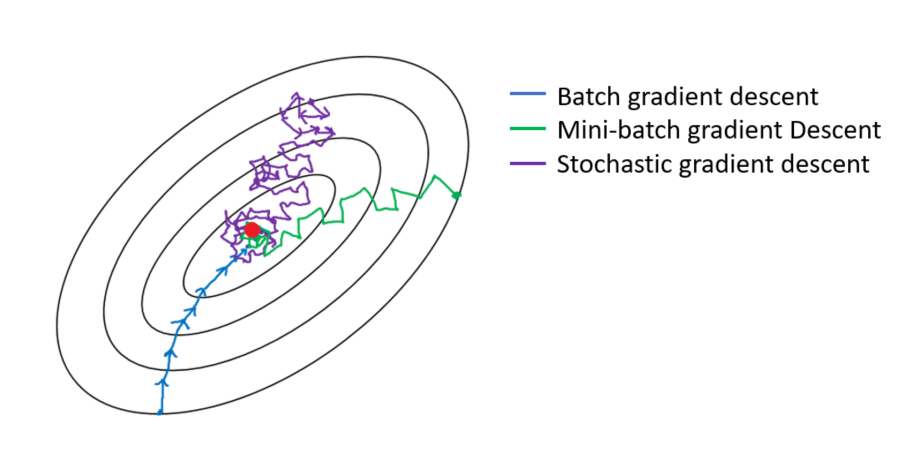
Supervised Learning - Ingredients

• Labelled data: \(\mathcal{D}\) (Experience, Task)
  
  

• Probabilistic Model: \(\pi_{w}( y \vert \boldsymbol{x})\) (Computer Program)
  
  

• Training approach:

  • Way to measure how good the model is (Performance)
  • Adapt \(w\) to improve such performance

Probabilistic Model

The shape of \(\pi_{w}( y \vert \boldsymbol{x})\) determines the model. Some important cases:

• Regression: \(y\in \mathbb{R}\) \[ \pi_{w}( y \vert \boldsymbol{x}) = \mathcal{N}(f_w(\boldsymbol{x}), \sigma) \]

• Classification: \(y \in \lbrace 1, \dots, K\rbrace\)

\[\begin{eqnarray*} \pi_{w}( y = i \vert \boldsymbol{x}, w) &=& p_i(\boldsymbol{x}, w) \\ p_i(\boldsymbol{x}, w) &=& \frac{e^{f_w(\boldsymbol{x})_i}}{\sum_{j=1}^K e^{f_w(\boldsymbol{x})_j}} \end{eqnarray*}\]

Linear models

For linear models \(f_w(\boldsymbol{x}) = w_1 x_1 + \dots w_p x_p\)

Very unflexible!

Beyond linearity - Neural Nets

Single layer and single neuron

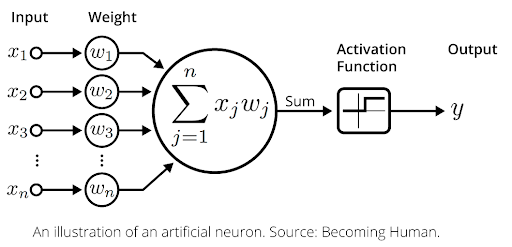
Beyond linearity - Neural Nets

Many layers and many neurons

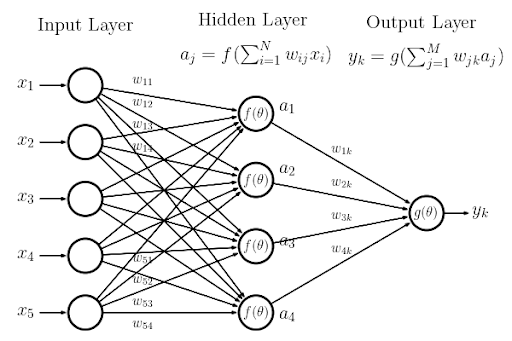
Beyond linearity - Neural Nets

• Neural Nets can in theory approximate any continuous function. [Innovative Models]

• [Automatic Differentiation] allows computing the gradient of the loss wrt the parameters very efficiently (same complexity as evaluating the function)

\[ w_{t+1} = w_t - \eta_{t} \cdot \nabla_w \ell (y_k, \boldsymbol{x}_k, w) \]

Supervised Learning - Ingredients

• Labelled data: \(\mathcal{D}\) (Experience, Task)
  
  

• Probabilistic Model: \(\pi_{w}( y \vert \boldsymbol{x})\) (Computer Program)
  
  

• Training approach:

  • Way to measure how good the model is (Performance)
  • Adapt \(w\) to improve such performance

Data

How to represent input data?

• Tabular

• Images

• Text

• Graphs

Data - Images

Represented as matrices, \(x_i\) corresponds to the intensity of the \(i\)-th pixel.

Data - Text

One hot encoding, \(x_i\) can take value 0 or 1.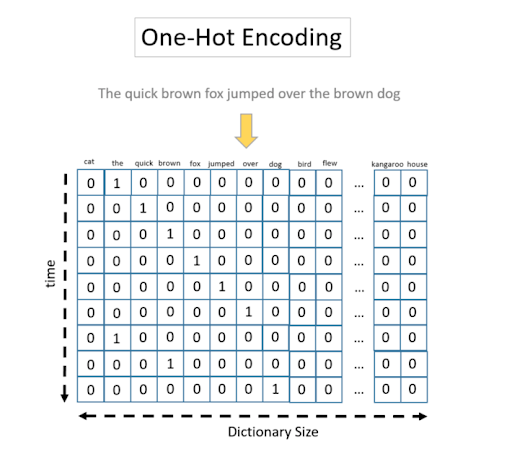

Data - More!

For instance graphs - Specific architectures (GNNs)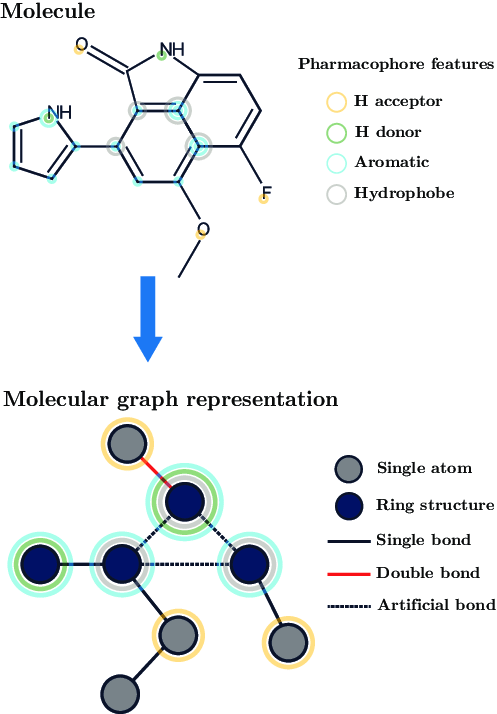

Data

Once images/text/graphs had been represented, rest of the procedure is the same:

1. Observed input-output pairs \(\mathcal{D} = \lbrace \boldsymbol{x}_i, y_i \rbrace_{i=1}^N\)

2. Choose a model \(\pi_{w}( y \vert \boldsymbol{x})\). This entails choosing \(f_w(\boldsymbol{x})\)

3. Choose a loss function \(L(\mathcal{D}, w)\)

4. Optimize to find \(w^*\): \(w_{t+1} = w_t - \eta_{t} \cdot \nabla_w L(\mathcal{D}, w)\)

5. Given new input \(\tilde{\boldsymbol{x}}\), predict using \(\pi_{w^*}( y \vert \tilde{\boldsymbol{x}})\)

Modern times - Self Supervision

• We are very good (in general) in supervised learning problems

• We need access to labelled \(\mathcal{D} = \lbrace \boldsymbol{x}_i, y_i \rbrace_{i=1}^N\)

• Most data in the internet is unlabelled…

• How can we create a supervised learning problem out of unlabelled data?

Modern times - Self Supervision

• Remove parts of the data (this will be our outcomes)

• Use the rest of data to predict the removed parts (features/inputs)

Modern times - GPT

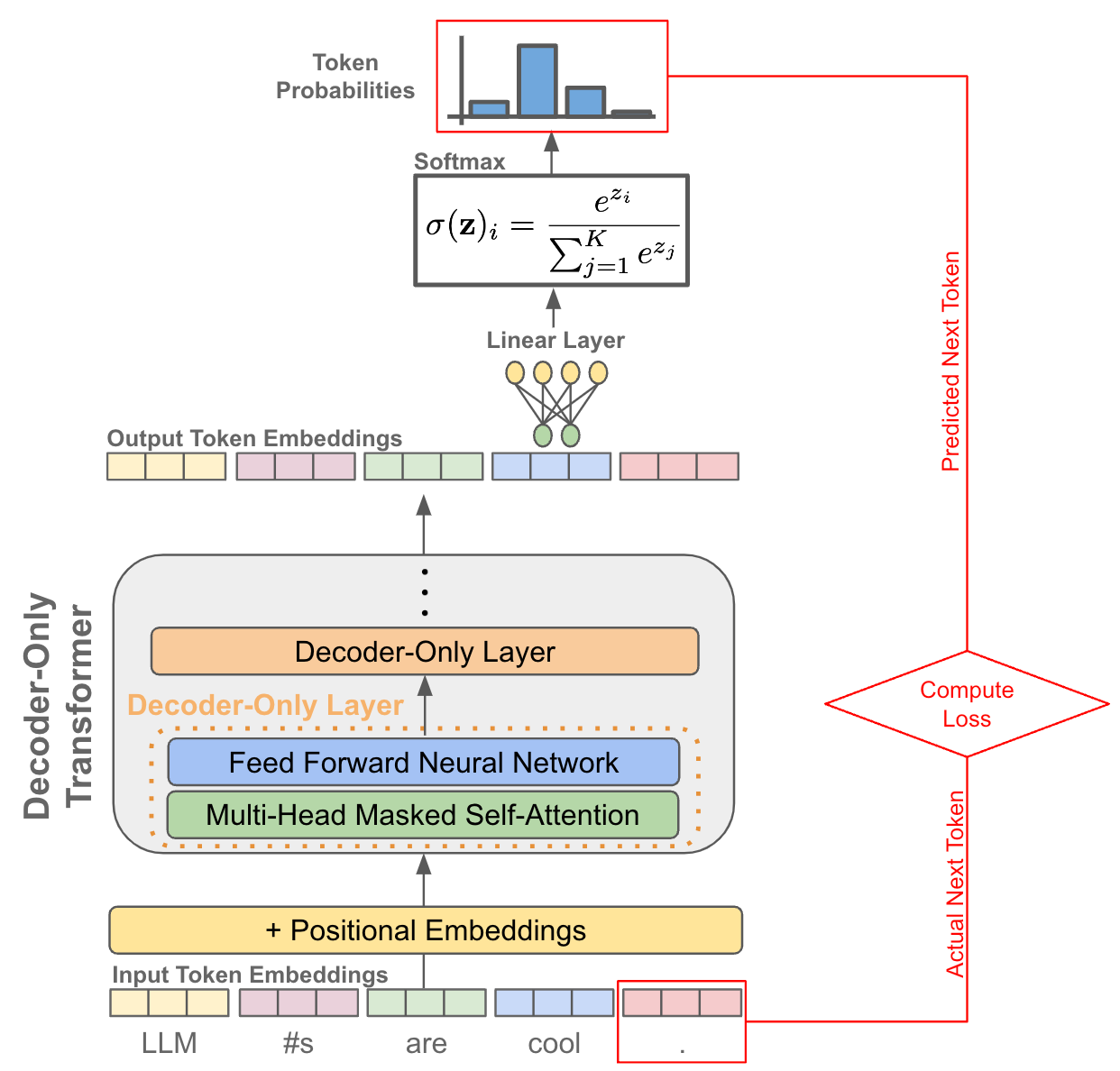
Some Random Thoughts

• Access to advanced ML models democratized by frameworks like PyTorch

• ML critically affects individual decision-making

  • Privacy? Democracy?

  • We are giving (very valuable data) for free!

• LLMs might eliminate many technical jobs, but not all

  • Safety, security?

• 4th Scientific Paradigm

Thank You!

Connect with me:

Twitter: @roinaveiro

Website: roinaveiro.github.io

Email: roi.naveiro@cunef.edu